The Fall of the Apple and the General Theory of Relativity
Can the basic concepts of the general theory of relativity be illustrated geometrically with almost no math? To answer this question, let's reconsider Newton's well-known problem of the falling apple.
The general theory of relativity (GTR) is one of the most fascinating theories because it not only has shattered the foundations of physics but also challenges our familiar view of the world. Although the mathematical formulation of GTR is rather demanding, it can be interpreted geometrically, thus providing deep insights in the nature of gravity.
The Apple and the Tree
We can illustrate the concept of the general theory of relativity by the example of an apple falling from a tree. Although the underlying problem can simply be solved using Newton’s famous formulas published at the end of the 17th century, these formulas are not able to explain why the apple falls towards the earth.
Another problem with Newton’s equations is that they predict an instant reaction of the falling mass if the gravitating mass is changed, which is clearly not the case. Even Newton was aware of these problems but he was not able to solve them. This was eventually done by Albert Einstein (1879-1955) more than 300 years later by introducing the famous general theory of relativity.
“The general theory of relativity can be explained by two simple principles.”
The GTR can be explained by two simple principles: The first principle is that matter curves spacetime, and the second is that a mass always follows a shortest path – a so called geodetic line – in the curved spacetime. We will start explaining the influence of matter on spacetime by the example of a mass that is being shot from the surface of the earth into the sky. Depending on the initial velocity v at the surface the mass reaches a highest point and then returns back to the earth.
An interesting question is whether we can increase the initial velocity v to a value such that the mass will never return to earth. The answer is yes; the required velocity to escape the gravitational field of the earth is the so called escape speed, which can be calculated simply by equating the kinetic energy Ekin and the potential energy Epot of the mass.
One then sees that this velocity depends on the gravitational constant and parameters as the mass and size of the earth. Here the question arises whether it is possible to change the parameters of the gravitating mass, i.e. the earth, such that the escape velocity equals the velocity of light. Again, the answer is yes. To achieve this, however, we would have to reduce the diameter of the earth to a tiny little ball with a radius as little as 1cm while keeping the mass constant.
Black holes and speed of light
In this case the earth would become a so called black hole from which not even light can escape. Although we are not going to discuss black holes in this article, this gedankenexperiment clearly shows that gravitation is even able to slowdown light.
Slowing down light by gravity, however, seems to be in contradiction to the well-known fact that the speed of light, called c, is constant.
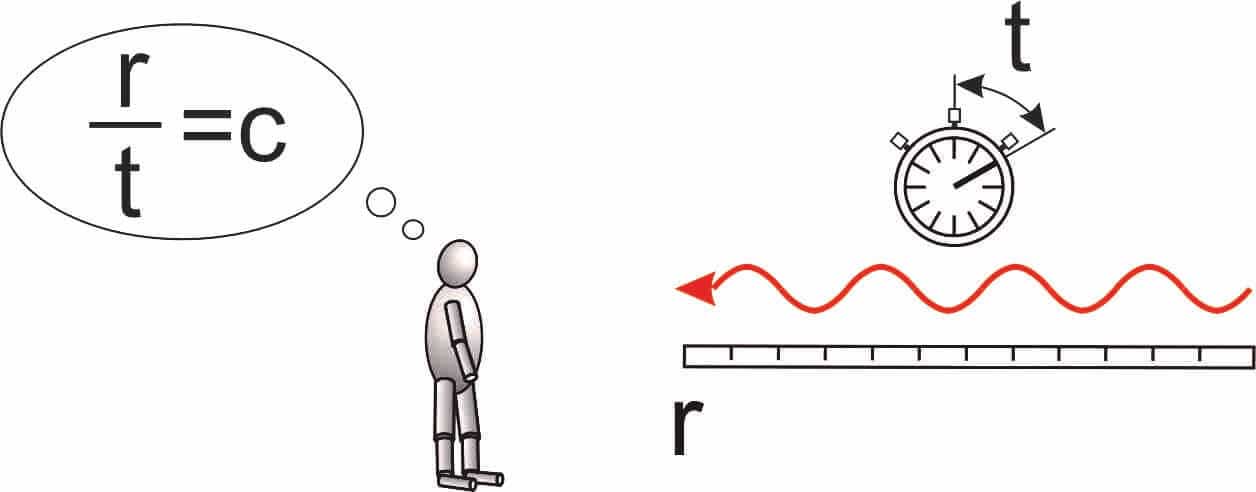
Namely, if an observer would measure the travel distance and the travel time of the light and then calculate the speed of the light, he would end up with a number less than c, which could not be correct.
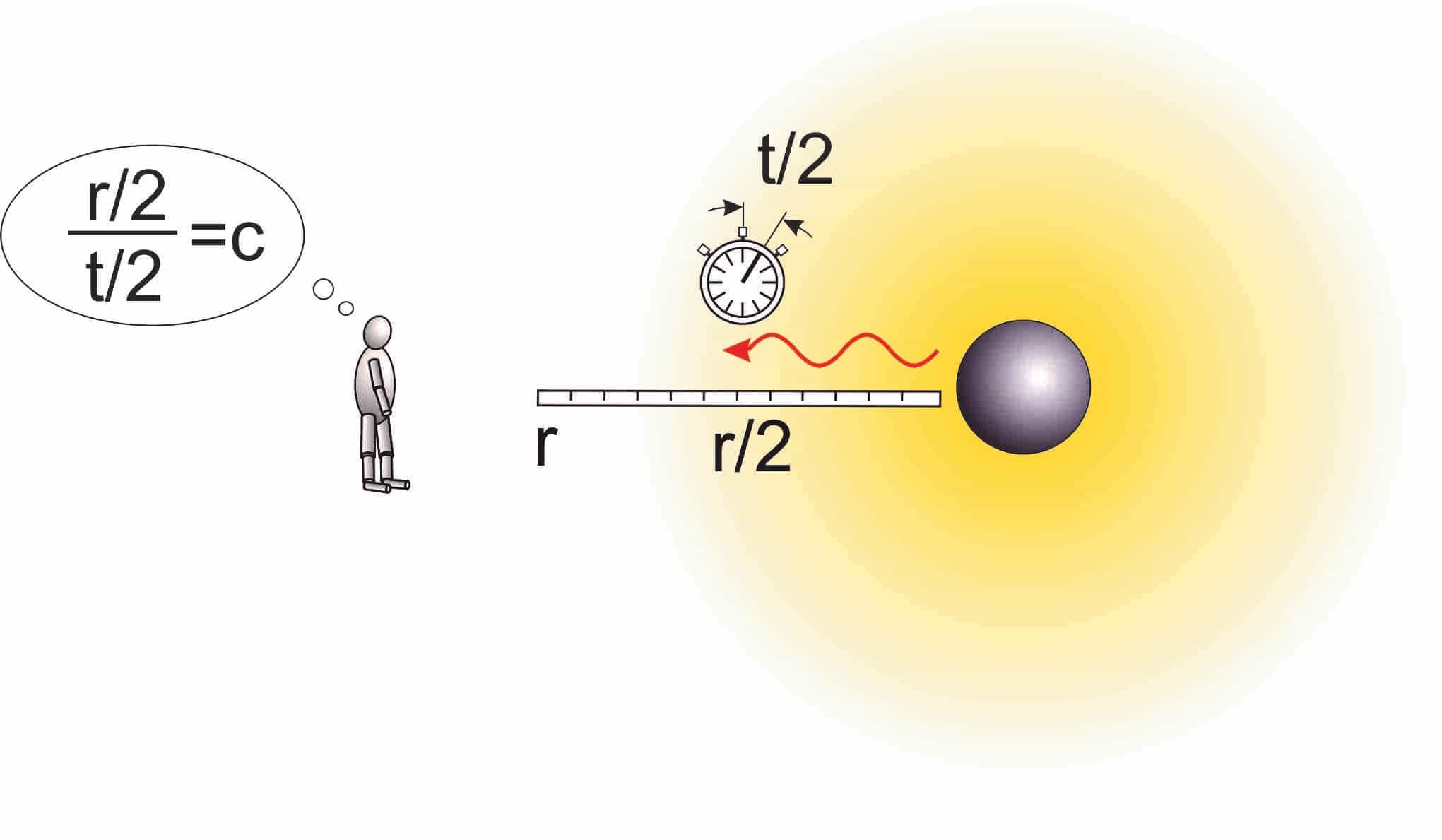
Einstein solved this problem with an ingenious nonetheless simple assumption: He said that gravitation also influences the time! Namely, a clock in a gravitational field slows down, such that the reduced travel distance of the light divided by the reduced travel time again equals the correct value c of the speed of light.
What is the consequence of slowing down time in a gravitational field? To answer this question we plot a so called spacetime diagram, i.e. a graph that simply shows the position r of a mass versus time t. In the absence of gravity, this diagram is a rectangular Cartesian coordinate system.
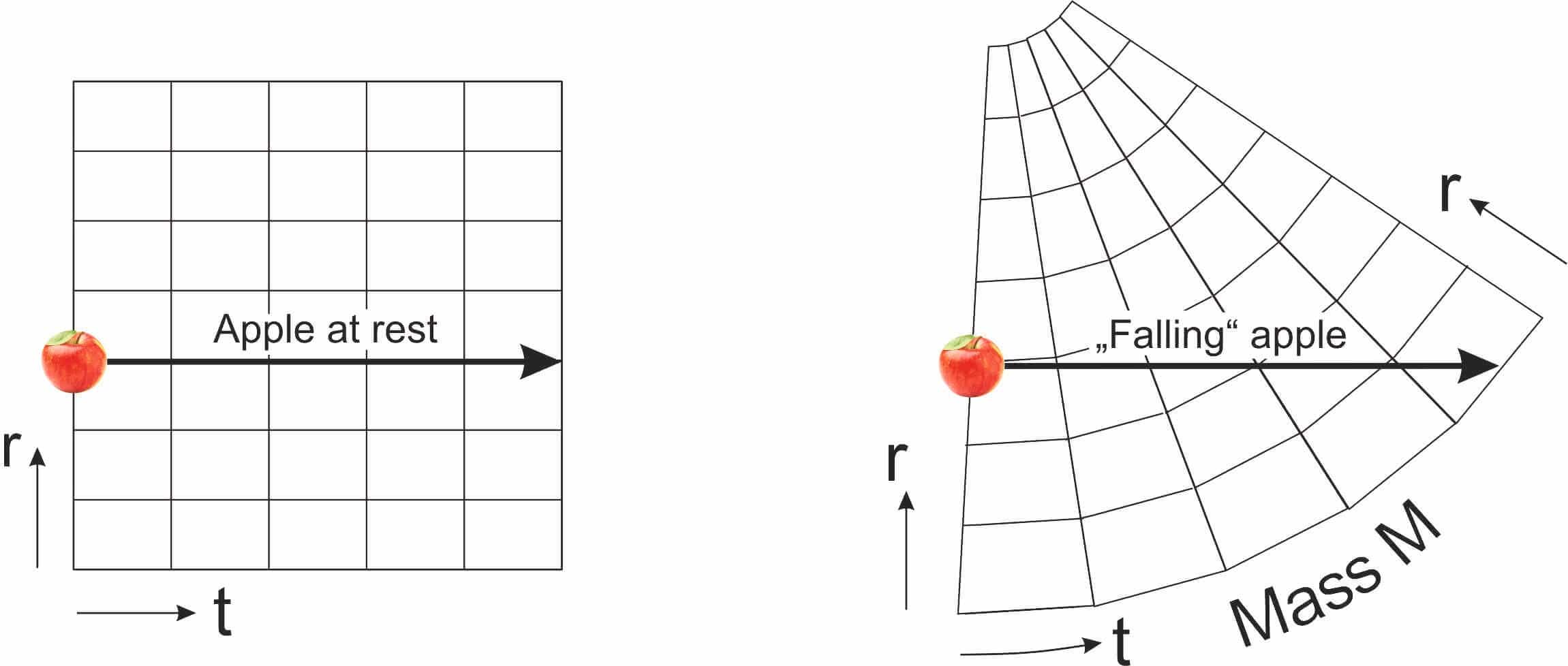
At first we investigate an apple without any (gravitational) force applied to it, which means that the apple stays at the same location r all the time, resulting in a straight, horizontal line (as shown in the above figure on the left). It should be noted that a straight line is the shortest connection between two points. We call such a line a geodetic line and it can be shown that a mass always follows a geodetic line even in a curved spacetime diagram.
Now, we take the influence of gravity into account, which means that the time in the vicinity of the gravitating mass M passes by slower, which can be illustrated by expanding the diagram in the time direction (as shown in the above figure on the right). This is exactly what is meant if one talks about “curved spacetime”. This illustrates the basic concept of the geometrical interpretation of gravity, although we used a simple example and we only considered one spatial dimension instead of three.
Apples in curved spacetime
To see what our apple is now doing in the curved spacetime, we again apply the principle of the “shortest path”, which means that we draw a straight line from the location of the apple at t=0 in horizontal direction. Obviously, under the influence of gravity, the apple begins to “fall” downwards. We can even see that the speed of the apple, which at each point is given by the change of r divided by the change of t, is zero at the beginning (t=0) and then increases while the apple moves towards the earth.
A thorough analysis which yields quantitative results, of course, requires more math. A central concept here is the curvature of multidimensional spaces which originally was introduced by Carl Friedrich Gauß (1777-1855) and then generalized by Bernhard Riemann (1826-1866). In conjunction with the so called metric that describes the structure of a multidimensional space, Einstein formulated his famous field equation, describing the influence of mass (or energy) on the metric, and thus on the structure of spacetime.
The metric in the vicinity of a spherical mass for example is a rather complicated mathematical structure, called Schwarzschild metric, that can be displayed only if one reduces the number of dimensions of the spacetime. Since in the case of the falling apple we only need one spatial coordinate r and the time coordinate t, the resulting metric can be illustrated by a two dimensional surface in the three-dimensional space, resulting in a tromp-like rotational symmetric sphere (see the figure below on the left).
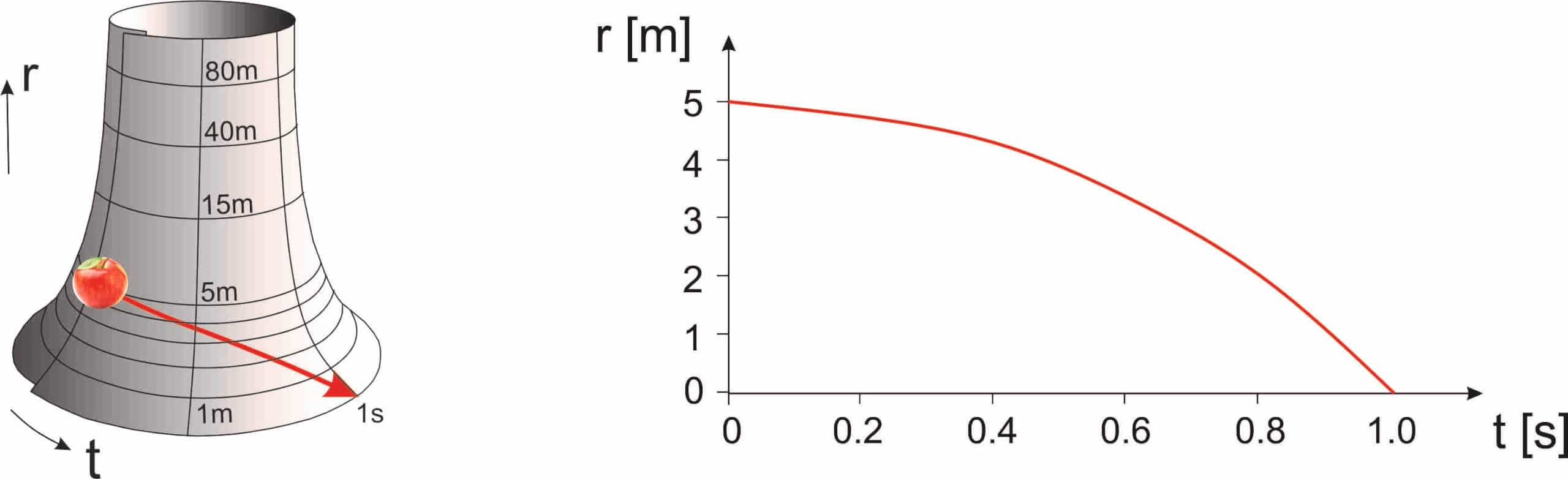
Applying the principle of the shortest path to this metric, we now can even extract the numerical values of the coordinates r and t, yielding the well-known parabolic curve of the falling apple under the influence of gravitation, as shown in the above figure on the right.
[Title image by Thomas Kelley (Creative Commons Zero), via Unsplash]
