Committee Theory, Or Finding Solutions to Problems That Have no Solution
By drawing several straight lines that cross one point on a piece of paper, we arrive at one of the most fascinating mathematical theories: Committee theory not only has a number of practical applications like pattern recognition - a central branch of machine learning - but also searches for collective solutions to problems that have no familiar solution at all.
Let’s take a blank piece of paper and a pencil. Let’s then draw a point and several straight lines, all crossing that point. All we have to do to arrive at the equally fascinating and complex committee theory is to prescribe a positive side, marked by small black triangles, to each line.
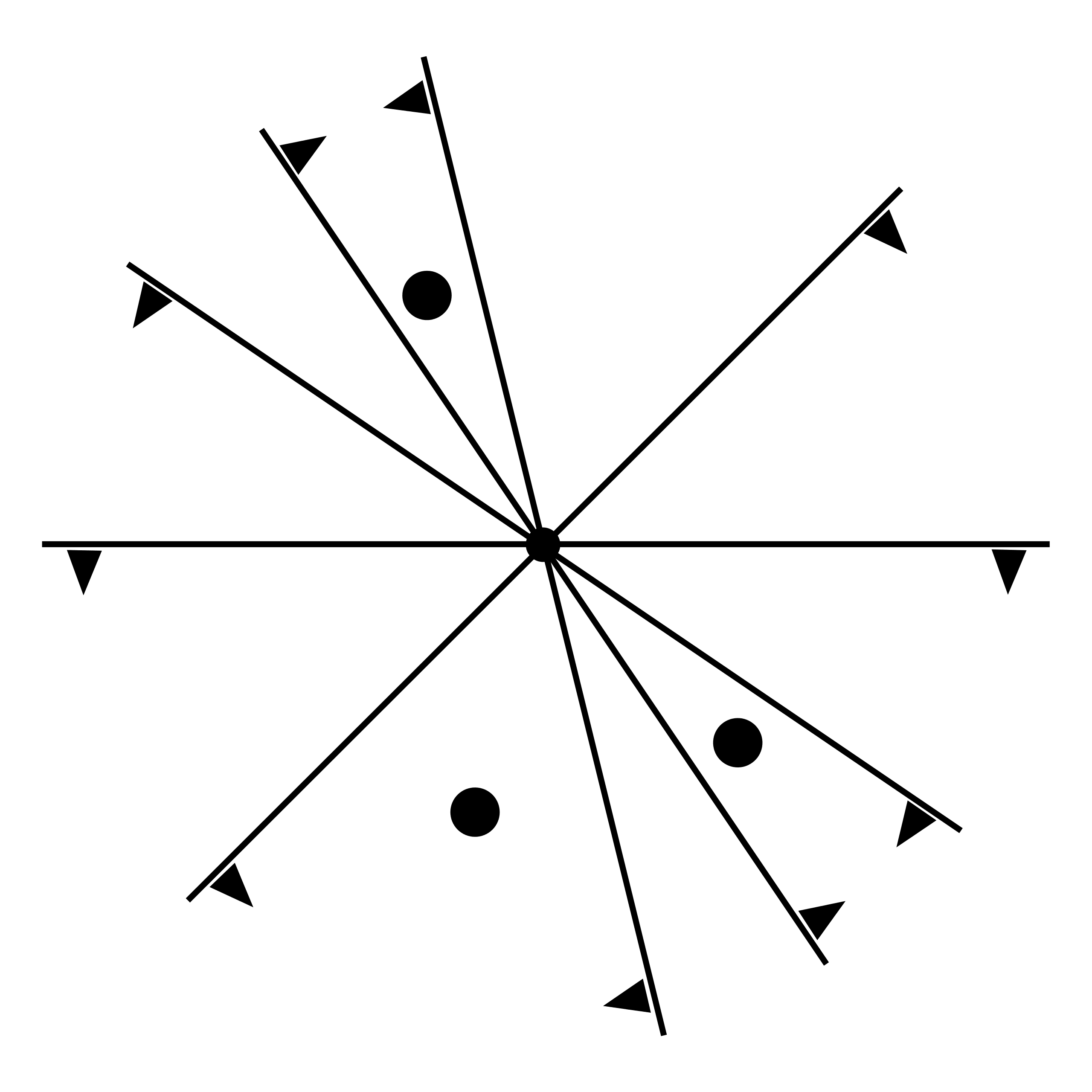
Every line now divides the paper into two halves, a positive side and a negative side. From a mathematical point of view, one such collection of lines can radically vary from another. This results in a different setting of problems that can be associated with such simple graphical arrangements. If someone were to find a point that lies on the positive sides of all lines, he or she would have found a solution to what mathematicians call an inequality system which the arrangement represents.
Enter Committee Theory
But what if there is – or seems to be – no such point? Arrangements in which points lying on the positive side of all lines cannot be found (like the example above), represent mathematical problems that are very hard to deal with. Enter modern committee theory: Its foundation was laid in 1965 by authors C.M. Ablow and D.J. Kaylor, who published an article on Inconsistent Homogeneous Linear Inequalities in the Bulletin of the American Mathematical Society. Ablow and Kaylor not only showed how to tackle inequality systems that have no familiar solutions, but also how one can construct collective solutions to almost any inequality system.
In the figure above we have been able to divide our piece of paper into positive and negative half-spaces by using straight lines only because this is a two-dimensional space. But the notion of an arrangement of separating surfaces applies to any higher dimension as well. We could be dealing with an arrangement of planes in our physical three-dimensional space.

Arriving at Solutions to Problems That Have no Solution
Mathematicians call the pizza slices seen in the first figure the regions of the arrangement. In fact, there is even a certain hierarchy of dialects in the language of mathematics for naming elementary pieces of arrangements, and such a hierarchy provides an excellent opportunity to take a fresh look at inequality systems – the standard working model for the two-class pattern recognition problem in its geometric setting.
“Even if we did not have a collective solution found for us in advance, we could easily create it ourselves.”
As noted above, our low-dimensional inequality system has no solution. However, something strange happens when you look at the black discs that mark three of the regions of the arrangement: for any line of the arrangement, there are two such regions which lie on the positive side of that line. In other words, a majority of marked regions is voting for every line.
In mathematical terms, someone pointed a collective solution to a system of linear constraints of our figure out for us. The good news is: even if we did not have such a collective solution found for us in advance, we could easily create it ourselves. It suffices to know a golden rule that works in flat contexts: one can construct a committee by collecting all those regions of the arrangement for each of which the two boundary black triangles both are pointing inside the region. And these are just a few basic facts and techniques of committee theory.
How to solve Pattern Recognition problems
To solve so called pattern recognition problems, software-hardware complexes first process some training data. These are collections of features, that is, quantitative parameters (for example: weight, blood pressure and blood sugar) together with labels of classes (like healthy and unhealthy) that are associated with the collections of features. The goal of processing such training sets is to let the machine learn to recognize new collections of parameters, that is, to relate each of them to one of the classes.
Suppose the two-dimensional space on our piece of paper was the feature space in a low-dimensional pattern recognition problem, and the arrangement in our first figure represented a training set given by the lines, each of which belongs to one of two classes. More precisely, the training lines (called training patterns) of one class were reoriented before their insertion into the arrangement. If we now add a new oriented line to the arrangement, then the corresponding pattern is recognized as a representative of one or another class on the basis of the result of the voting procedure performed by the members of a committee of the arrangement.
